Площадь выпуклого четырёхугольника

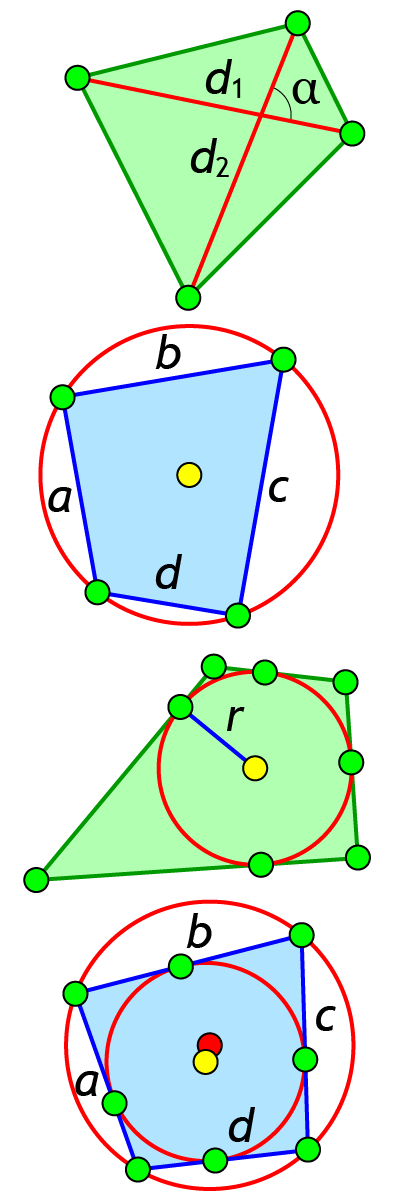
• Пусть у выпуклого четырёхугольника длины сторон равны a, b, c, d, полупериметр равен p, радиус вписанной окружности равен r, диагонали равны d₁ и d₂, а угол между ними равен $α$.

• Площадь выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними:

$S=\frac{1}{2}{d}_1{d}_2\sin \mathrm{\alpha }.$

• Если в четырёхугольник можно вписать окружность, то его площадь можно найти по формуле Брахмагупты:

$S=\sqrt{\left(p - a\right)\left(p - b\right)\left(p - c\right)\left(p - d\right)}.$

• Если четырёхугольник можно вписать в окружность, то его площадь вычисляется по формуле:

$S=pr.$

• Если около четырёхугольника можно описать окружность, а также вписать в него окружность, то его площадь равна:

$S=\sqrt{abcd}.$